机器学习日记01

01 概念

什么是机器学习？在这里插入图片描述 T:任务，目的，结果 E:训练集，经验值 h：假设，方程 p：置信区间

一个程序被认为能从经验E中学习, 解决任务T，达到性能度量值P，当且仅当，有了经验E后，经过P评判，程序在处理T时的性能有所提升。 我认为经验E就是程序上万次的自我练习的经验而任务，T是下棋。性能度量值P呢，就是它在与一些新的对手比赛时，赢得比赛的概率。

更经典的定义：

一个计算机程序利用经验E来学习任务T，性能是P，如果针对任务T的性能P随着经验E不断增长，则称为机器学习。

汤姆·米切尔（Tom Mitchell），1997

机器学习实战：基于Scikit-Learn、Keras和TensorFlow：原书第2版中文版

特点

  • 有解决方案（但解决方案需要进行大量人工微调或需要遵循大量规则）的问题：机器学习算法通常可以简化代码，相比传统方法有更好的性能
  • 传统方法难以解决的复杂问题：最好的机器学习技术也许可以找到解决方案。
  • 环境有波动：机器学习算法可以适应新数据。
  • 洞察复杂问题和大量数据。

基本概念

有监督学习和无监督学习 有监督学习: 我们将教计算机如何去完成任务

无监督学习中:我们打算让它自己进行学习

此外你将听到诸如，强化学习和推荐系统等各种术语。这些都是机器学习算法的一员

监督学习

监督学习指的就是我们给学习算法一个数据集。这个数据集由“正确答案"组成。在房价的例子中,我们给了一系列房子的数据,我们给定数据集中每个样本的正确价格 在预测类的问题中，监督学习的过程是给予数据集，设置假设，计算预测

回归&分类&其他

回归这个词的意思是，我们在试着推测出这一系列连续值属性。

分类指的是，我们试着推测出离散的输出值：0或1良性或恶性，而事实上在分类问题中，输出可能不止两个值。比如说可能有三种乳腺癌，所以你希望预测离散输出

我们以后会讲 一个算法，叫支持向量机，里面有一个巧妙的数学技巧，能让计算机处理无限多个特征。

总结

现在来回顾一下，这节课我们介绍了监督学习。其基本思想是，我们数据集中的每个样本都有相应的 “正确答案 ”。 再根据这些样本作出预测 就像房子和肿瘤的例子中做的那样 。我们还介绍了回归问题，即通过回归来推出一个连续的输出，之后我们介绍了分类问题，其目标是推出一组离散的结果。

无监督学习

两种列举的无监督学习

无监督学习算法可能会把这些数据分成两个不同的簇。所以叫做聚类算法。事实证明，它能被用在很多地方。

鸡尾酒宴会——另外一种方法

02 正题：单变量线性回归

回归 一词指的是，我们根据之前或者已有的数据预测出一个准确的输出值

对一般回归问题的标记

在这里插入图片描述 在这里插入图片描述 我将选择最初的使用规则ℎ代表 hypothesis，因而，要解决房价预测问题，我们实际上是要将训练集 “喂 ”给我们的学习算法 进而学习得到一个假设 ℎ，然后将我们要预测的房屋的尺寸作为输入变量输入给 ℎ，预测出该房屋的交易价格作为输出变量输出为结果。

一种可能的表达方式为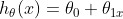：在这里插入图片描述 ​​，因为只含有一个特征 /输入变量，因此这样的问题叫作单变量线性回归问题。 #### 代价函数 因为我们设置的h只是一种假设，因此通过假设方程预测的数与真值一定有偏差，将已知的真值与通过假设方程的差异展现出来的方程叫做代价函数

在优化类数模模型中：

一个最佳化问题的目标是将损失函数最小化。

代价函数的常见形式是最小二乘法 模型所预测的值与训练集中实际值之间的差距（下图中蓝线所指）就是 建模误差 modeling error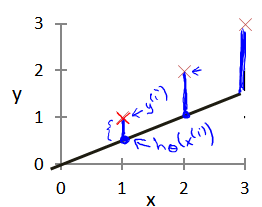） 在这里插入图片描述 我们的目标便是选择出可以使得建模误差的平方和能够最小的模型参数。即使得代价函数最小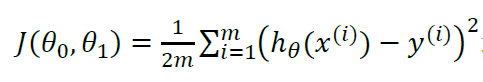代价函数

损失函数的图形化表示

𝐽(𝜃0,𝜃1) 就是代价函数，也称损失函数 𝐽(𝜃1) 是二维的函数关系 𝐽(𝜃0,𝜃1) 是三维的函数关系

在这里插入图片描述 #### 损失函数存在的意义 在这里插入图片描述 为了使得求得的预测值与真值差距最小化，在损失函数中应当找到函数的极小值

如何找到极小值，一般有两种方法，一个叫梯度下降，另一个叫normal equation，下面先讲梯度下降

梯度下降

梯度下降——梯度下降是一个用来求函数最小值的算法，我们将使用梯度下降算法来求出代价函数𝐽(𝜃0,𝜃1) 的最小值。

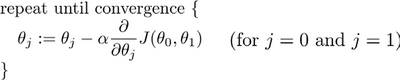梯度下降背后的思想是：开始时我们随机选择一个参数的组合 (𝜃0,𝜃1,......,𝜃𝑛)，计算代价函数，然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到到到一个局部最小值（ local minimum），因为我们并没有尝试完所有的参数组合，所以不能确定我们得到的局部最小值是否便是全局最小值（ global minimum），选择不同的初始参数 组合，可能会找到不同的局部最小值。 在这里插入图片描述 批量梯度下降（ batch gradient descent）算法的公式为 在这里插入图片描述 其中 𝑎是学习率（ learning rate），它决定了我们沿着能让代价函数下降程度最大的方向 向下迈出的步子有多大，在批量梯度下降中，我们每一次都同时让所有的参数减去学习速率 乘以代价函数的导数。 在这里插入图片描述 对于这个问题，求导的目的，基本上可以说取这个红点的切线，就是这样一条红色的直线，刚好与函数相切于这一点，让我们看看这条红色直线的斜率，就是这条刚好与函数曲线相切的这条直线，这条直线的斜率正好是这个三角形的高度除以这个水平长度，现在，这条线有一个正斜率，也就是说它有正导数，因此，我得到的新的 𝜃1 𝜃1更新后等于 𝜃1减去一个正数乘以 𝑎。

如果𝑎太小了，即我的学习 速率太小，结果就是只能这样像小宝宝一样一点点地挪动，去努力接近最低点，这样就需要很多步才能到达最低点，所以如果 𝑎太小的话，可能会很慢，因为它会一点点挪动，它会需要很多步才能到达全局最低点。

如果𝑎太大，那么梯度下降法可能会越过最低点，甚至可能无法收敛，下一次迭代又移动了一大步，越过一次，又越过一次，一次次越过最低点，直到你发现实际上离最低点越来yuan

梯度下降python实现，BGD
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
# _*_ coding: utf-8 _*_
# 作者: yhao
# 博客: http://blog.csdn.net/yhao2014
# 邮箱: yanhao07@sina.com
 
# 训练集
# 每个样本点有3个分量 (x0,x1,x2)
x = [(1, 0., 3), (1, 1., 3), (1, 2., 3), (1, 3., 2), (1, 4., 4)]
# y[i] 样本点对应的输出
y = [95.364, 97.217205, 75.195834, 60.105519, 49.342380]
 
# 迭代阀值，当两次迭代损失函数之差小于该阀值时停止迭代
epsilon = 0.0001
 
# 学习率
alpha = 0.01
diff = [0, 0]
max_itor = 1000
error1 = 0
error0 = 0
cnt = 0
m = len(x)
 
# 初始化参数
theta0 = 0
theta1 = 0
theta2 = 0
 
 
 
 
while True:
    cnt += 1
 
    # 参数迭代计算
    for i in range(m):
        # 拟合函数为 y = theta0 * x[0] + theta1 * x[1] +theta2 * x[2]
        # 计算残差
        diff[0] = (theta0 + theta1 * x[i][1] + theta2 * x[i][2]) - y[i]
 
        # 梯度 = diff[0] * x[i][j]
        theta0 -= alpha * diff[0] * x[i][0]
        theta1 -= alpha * diff[0] * x[i][1]
        theta2 -= alpha * diff[0] * x[i][2]
 
    # 计算损失函数
    error1 = 0
    for lp in range(len(x)):
        error1 += (y[lp] - (theta0 + theta1 * x[lp][1] + theta2 * x[lp][2])) ** 2 / 2
 
    if abs(error1 - error0) < epsilon:
        break
    else:
        error0 = error1
 
    print("theta0 : %f, theta1 : %f, theta2 : %f, error1 : %f" % (theta0, theta1, theta2, error1))
print('Done: theta0 : %f, theta1 : %f, theta2 : %f' % (theta0, theta1, theta2))
print('迭代次数: %d' % cnt)
#为什么相邻两个残差相差在0.0001说明我们能够找到全局最优解呢？因为根据梯度下降的原理，每一次迭代过程我们得到的m个theta必然越来越接近最优解的，相差0.0001说明m个theta无法继续下降

梯度下降的表现形式

在这里插入图片描述 在梯度下降算法中，这是正确实现同时更新的方法。我不打算解释为什么你需要同时更新，同时更新是梯度下降中的一种常用方法。我们之后会讲到，同步更新是更自然的实现方法。当人们谈到梯度下降时，他们的意思就是同步更新。

梯度下降的进一步理解

梯度下降算法如下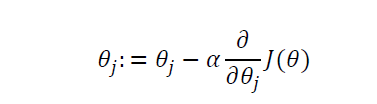： 在这里插入图片描述 描述：对 𝜃赋值，使得 𝐽(𝜃)按梯度下降最快方向进行，一直迭代下去，最终得到局部最小值。其中 𝑎是学习率（ learning rate），它决定了我们沿着能让代价函数下降程度最大的方 向向下迈出的步子有多大

求导能够把函数化简 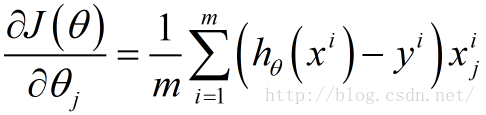在这里插入图片描述

线性回归与梯度下降

梯度下降与线性回归算法 在这里插入图片描述 在这里插入图片描述

现在我们已经掌握了梯度下降，我们可以在不同的环境中使用梯度下降法，我们还将在 不同的机器学习问题中大量地使用它。所以，祝贺大家成功学会你的第一个机器学习算法。

#机器学习
机器学习日记01
http://example.com/2021/07/12/机器学习笔记01/
作者
Brianyjh
发布于
2021年7月12日
许可协议