机器学习中的分类问题

前言

这周我们参考的是《机器学习实战：基于Scikit-Learn、Keras和TensorFlow》第三章的内容，进行对于分类问题的探讨，本文你将学会的知识：

1. 机器学习中（其他）适用于分类的性能度量方法
2. 多分类策略
3. 涉及多分类问题的性能度量
4. 多标签与多输出分类

mnist数据集(二分类)

我们本次训练的数据是著名的mnist数据集，从mnist.keys()我们可以看到其包含的内容

from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784',version=1,as_frame=False)
mnist.keys()
#dict_keys(['data', 'target', 'frame', 'categories', 'feature_names', 'target_names', 'DESCR', 'details', 'url'])

X, y =mnist['data'],mnist['target']
X.shape
# (70000, 784)

mnist数据集的基本信息

mnist数据集是NIST（National Institute of Standards and Technology，美国国家标准与技术研究所）数据集的一个子集

使用mnist.keys()返回9个key名字

data：图片数据

target：图片对应的字

frame: NoneType

categories:无

feature_names：数据集每个特征名字

target_names：target数据的名称

DESCR：来源信息

details：详细信息

url：数据集网站

7万张图片，每张图片28×28=784个特征，每个特征代表了每个像素点的强度，从0到255

划分数据

mnist数据集实际上已经将数据进行了合理的划分——前60000个数据为训练集，后面的是测试集

我们进行二元分类，模型用于判断是否是5

X_train, X_test, y_train, y_test =X[:60000],X[60000:], y[:60000], y[60000:]
y_train_5 = (y_train ==5)
y_test_5 = (y_test==5)

SGD分类

在这里我们构建SGDclassify分类器，

from  sklearn.linear_model import SGDClassifier

sgd_clf = SGDClassifier(random_state=42)
sgd_clf.fit(X_train,y_train_5)
# SGDclassify Stochastic Gradient Descent 梯度下降分类

交叉验证

在这里，我们使用3折交叉验证度量模型的性能，

from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf,X_train,y_train_5,cv=3,scoring='accuracy')
# array([0.95035, 0.96035, 0.9604 ])

这里返回3折交叉验证的准确率得分，我们可以看到都大于95%

但是mnist只有一小部分的图片是数字5，因此造成了非常严重的数据不均衡问题

我们可以从下面一个例子进行验证

from sklearn.base import BaseEstimator
class Never5Classifer(BaseEstimator):
    def fit(self,X,y=None):
        pass
    def predict(self,X):
        return np.zeros((len(X),1),dtype=bool)

never_5_clf =Never5Classifer()
cross_val_score(never_5_clf,X_train,y_train_5,cv=3,scoring='accuracy')
#array([0.91125, 0.90855, 0.90915])

在上面的例子中，我们构建了一个永远只输出False的模型never_5_clf，即便是只输出False，我们可以发现准确率仍然是0.90以上。

因此此前使用准确率对模型性能进行判断不能说明模型有多好。

因此我们再会尝试使用混淆矩阵进行性能评估

混淆矩阵

混淆矩阵Confusion Matrix也称误差矩阵，是表示精度评价的一种标准格式，用n行n列的矩阵形式来表示^[1]

在图像精度评价中，主要用于比较分类结果和实际测得值，可以把分类结果的精度显示在一个混淆矩阵里面。

混淆矩阵的结构一般如下图表示的方法。

混淆矩阵要表达的含义：

• 混淆矩阵的每一列代表了预测类别，每一列的总数表示预测为该类别的数据的数目；
• 每一行代表了数据的真实归属类别，每一行的数据总数表示该类别的数据实例的数目；每一列中的数值表示真实数据被预测为该类的数目。

True Positive（TP）：真正类。样本的真实类别是正类，并且模型识别的结果也是正类。

False Negative（FN）：假负类。样本的真实类别是正类，但是模型将其识别为负类。

False Positive（FP）：假正类。样本的真实类别是负类，但是模型将其识别为正类。

True Negative（TN）：真负类。样本的真实类别是负类，并且模型将其识别为负类。

该矩阵可用于易于理解的二类分类问题，但通过向混淆矩阵添加更多行和列，可轻松应用于具有3个或更多类值的问题。

从混淆矩阵当中，可以得到更高级的分类指标：Accuracy（正确率），Precision（精度或者准确率），Recall（召回率），Specificity（特异性），Sensitivity（灵敏度）。

正确率Accuracy：

\[ \text{准确率}=\frac{TP+FP}{TP+FP+FP+TN} \]

精度或查准率Precision：

\[ \text{精度}=\frac{TP}{TP+FP} \]

召回率Recall：

\[ \text{召回率}=\frac{TP}{TP+FN} \]

将Recall和Precision结合，可以组成F1度量，用于判断查准查全的性能

F1度量是Recall和Precision的调和平均值:

当Recall和Precision同时高时，F1才会高

\[ F_1=\frac{2}{\frac{1}{\text{查准率}}+\frac{1}{\text{召回率}}}=2\times \frac{\text{查准率}\times \text{召回率}}{\text{查准率}+\text{召回率}}=\frac{2\times TP}{\text{范例总数}+TP-TN} \]

Fβ是是Recall和Precision的加权调和平均值：

\[ F_{\beta}=\frac{\left( 1+\beta ^2 \right) \times \text{查准率}\times \text{召回率}}{\left( \beta ^2\times \text{查准率} \right) +\text{召回率}} \]

\(\beta\) 反映查全率相对于查准率的重要性： \(\beta=1\)退化为标准的F1,\(\beta>1\)查全更重要，\(\beta<1\)查准率更重要

对于不同的训练背景，对查全率与查准率有不同的要求，例如推荐系统认为查准率更重要，重要物品信息检索系统认为查全率更重要。

我们构建混淆矩阵：

from sklearn.model_selection import cross_val_predict
y_train_pred =cross_val_predict(sgd_clf,X_train,y_train_5,cv=3)
from sklearn.metrics import confusion_matrix
confusion_matrix(y_train_5, y_train_pred)
#array([[53892,   687],
#      [ 1891,  3530]], dtype=int64)

精度或查准率Precision：

from sklearn.metrics import precision_score, recall_score
precision_score(y_train_5,y_train_pred)
#0.8370879772350012

召回率Recall：

recall_score(y_train_5,y_train_pred)
#0.6511713705958311

F1度量：

from  sklearn.metrics import f1_score
f1_score(y_train_5,y_train_pred)

从上面几个指标的表现来看，模型的训练结果并不是特别好，只有65.12%的数字5被检测出来。

我们还可以通过观察通过改变阈值来改变查准率和查全率，并观察整个变化过程：

查准率/召回率的权衡

SGDClassifier模型会对每个实例，基于决策函数计算出一个值，如果该值大于阈值，将实例判断为正类，否则判断为负类，改变阈值将会影响正负类各自的个数，提高阈值可能会提高精度，降低召回率。

利用decision_function方法，能够得到决策分数

from sklearn.model_selection import cross_val_predict
y_scores = cross_val_predict(sgd_clf,X_train,y_train_5,cv=3,method='decision_function')

使用precision_recall_curve根据上面求出的决策分数，得出计算不同概率阈值的查准率/召回率对，可以画出来：

def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
    plt.plot(thresholds,precisions[:-1],'b--',label="Precisions",linewidth=2)
    plt.plot(thresholds,recalls[:-1], 'g-',label='Recall',linewidth=2)
    plt.legend(loc='center right', fontsize=16)
    plt.xlabel('Threshold',fontsize=16)
    plt.grid(True)
    plt.axis([-50000,50000, 0, 1])
recall_90_precision = recalls[np.argmax(precisions >=0.90)]
threshold_90_precision = thresholds[np.argmax(precisions>=0.90)]

plt.figure(figsize=(8,4))
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
plt.plot([threshold_90_precision,threshold_90_precision],[0.,0.9],'r:')
plt.plot([-50000,threshold_90_precision],[0.9,0.9],'r:')
plt.plot([-50000,threshold_90_precision],[recall_90_precision,recall_90_precision],'r:')
plt.plot([threshold_90_precision],[0.9],'ro')
plt.plot([threshold_90_precision],[recall_90_precision],'ro')
save_fig('precision_recall_vs_threshold_plot')
plt.show()![precision_recall_vs_threshold_plot](E:\blog\source\images\20221029\precision_recall_vs_threshold_plot.png)

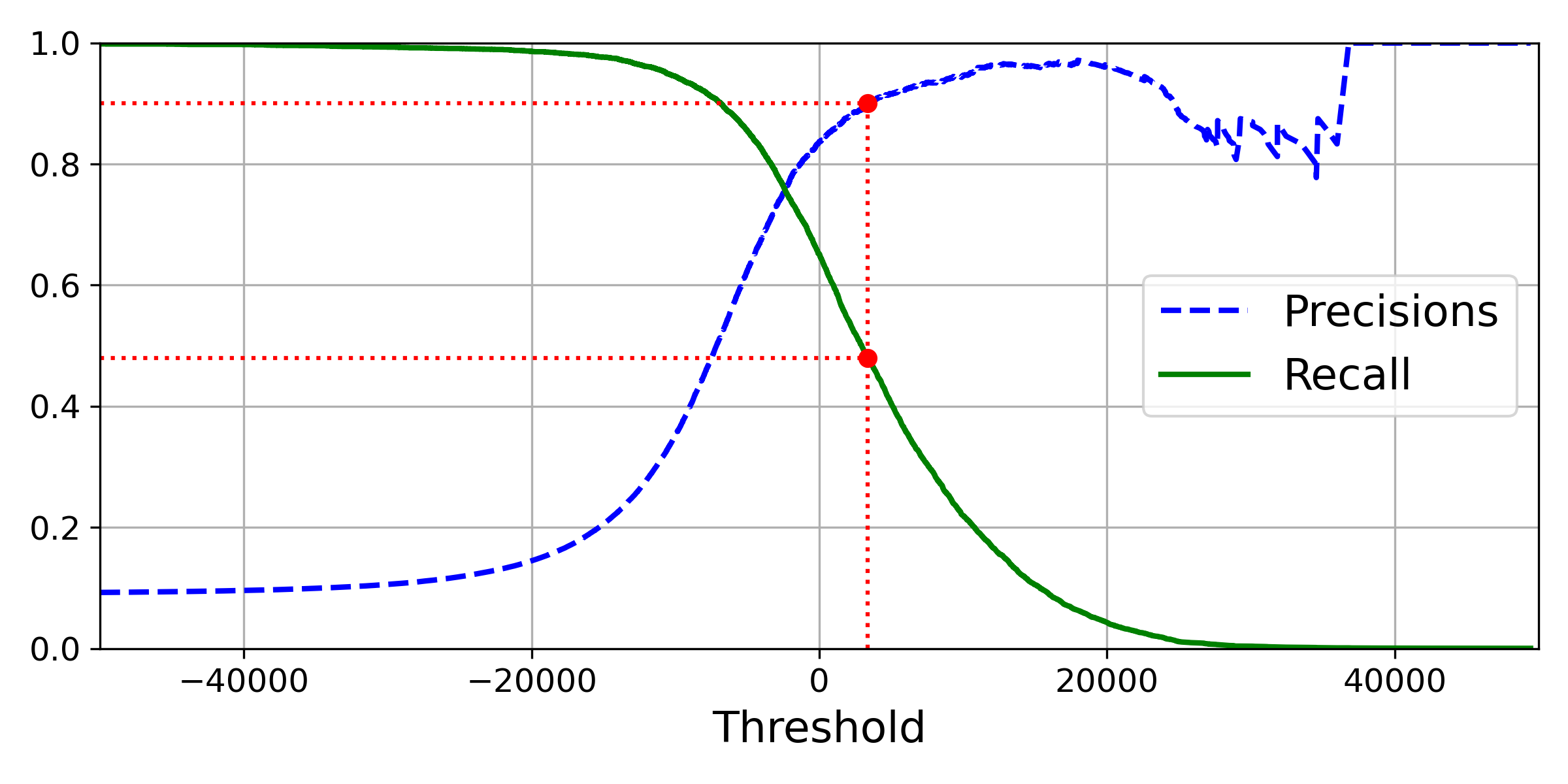
通过上面的图我们可以看出随着阈值Threshold的变化，查准率和召回率的变化，在图中，我们还可以看到查准率随着阈值提高会发生波动，例如，假设阈值提高一点点之后，并没有把非5法数字除去，反而去除了数字5的例子，会造成查准率的降低。

我们还可以画图查看查准率和查全率的关系：

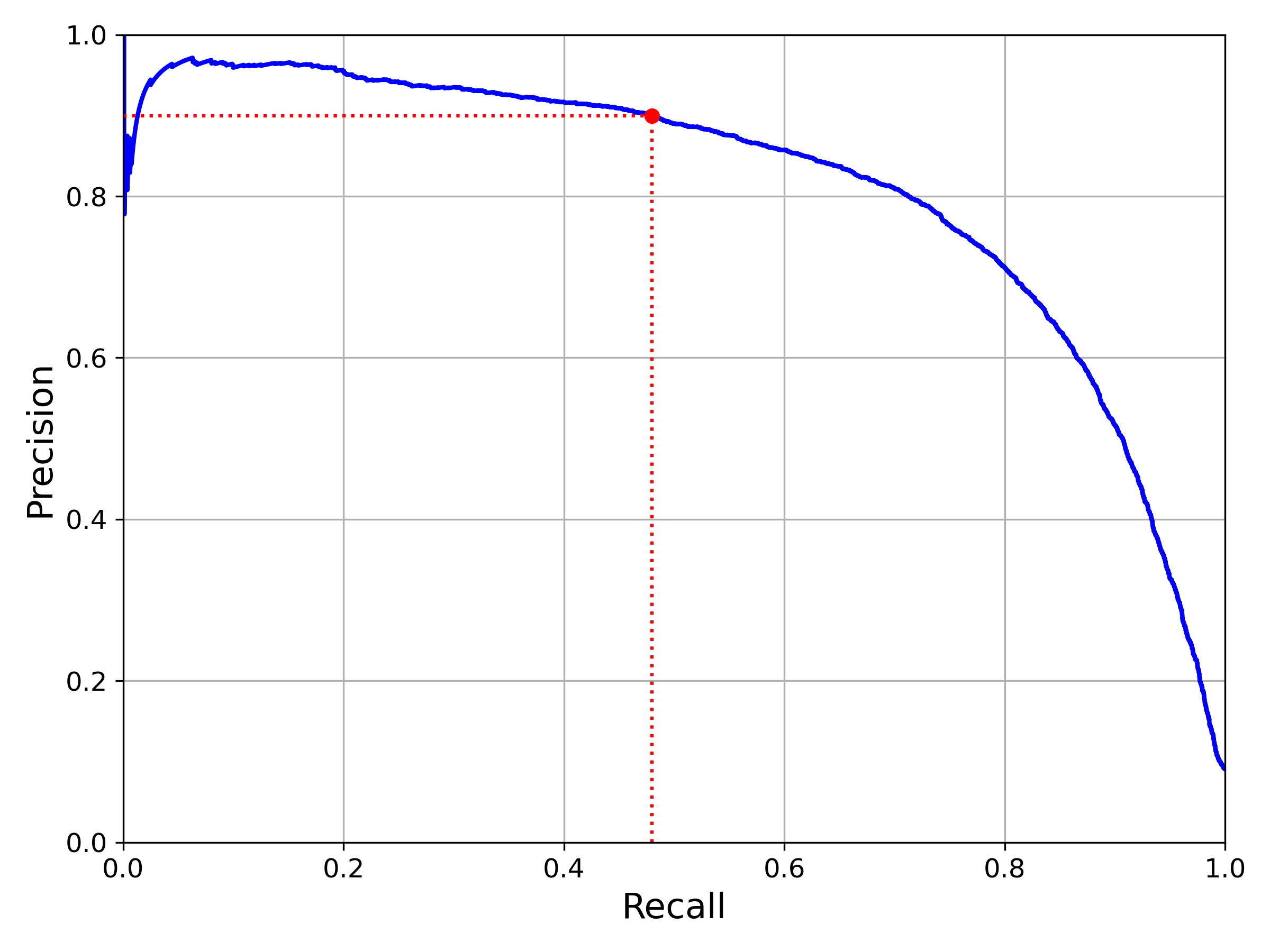
ROC曲线

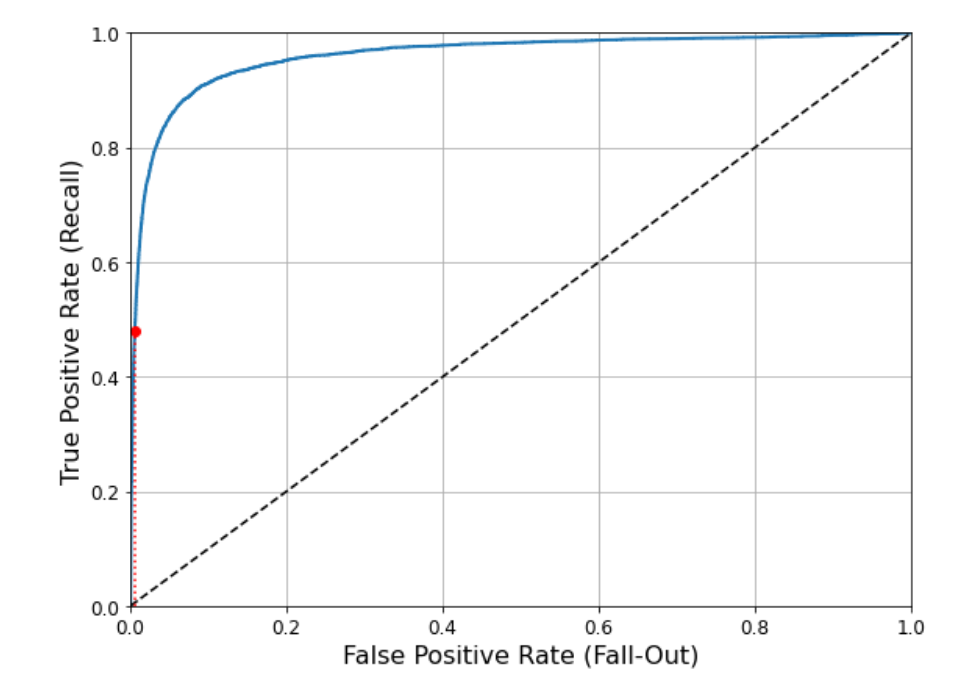
ROC曲线，即受试者工作特征曲线，与查准率/召回率曲线非常相似，绘制的是真正类率（即原来的召回率，也叫灵敏度）和假正类率（FPR）。FPR又称为特异度，是错误被分成正类的负类实例比例，等于正确分类成负类的负类实例比例。

from sklearn.metrics import roc_curve

fpr,tpr, thresholds =roc_curve(y_train_5,y_scores)

召回率越高，分类器产生的假正类类越多，虚线表示纯纯随机的分类器的ROC曲线，一个优秀的分类器应远离这条线

image-20221101214240997

多分类问题

对于多分类的策略，常常有俩个策略^[2]：

OvR策略是一种一对多策略，每次将一类的样例作为正例、其他所有数据作为反例来进行数据集拆分。对于三分类问题，会分成：

判断是否是0的二元分类器 以及相应得分 判断是否是1的二元分类器 以及相应得分 判断是否是2的二元分类器 以及相应得分

最后选取得分最高的

OvO策略是一种一对一策略，OvO的拆分策略比较简单，基本过程是将每个类别对应数据集单独拆分成一个子数据集，然后令其两两组合，再来进行模型训练。例如，对于上述三分类数据集，根据标签类别可将其拆分成三个数据集，然后再进行两两组合，总共有3种组合

OvO策略适用于较小数据量的分类任务

创建OVR分类器：

from sklearn.multiclass import OneVsRestClassifier
ovr_clf = OneVsRestClassifier(SVC(gamma='auto',random_state=42))#基于SVC创建多类分类器
ovr_clf.fit(X_train[:1000],y_train[:1000])

误差分析（多分类）

对于多分类问题，我们为了了解他的性能，可以制作其混淆矩阵：

from sklearn.model_selection import cross_val_predict
y_train_pred = cross_val_predict(sgd_clf,x_train_scaled,y_train,cv=3)
from sklearn.metrics import confusion_matrix
conf_mx=confusion_matrix(y_train,y_train_pred)
conf_mx

得到混淆矩阵

array([[5577,    0,   22,    5,    8,   43,   36,    6,  225,    1],
       [   0, 6400,   37,   24,    4,   44,    4,    7,  212,   10],
       [  27,   27, 5220,   92,   73,   27,   67,   36,  378,   11],
       [  22,   17,  117, 5227,    2,  203,   27,   40,  403,   73],
       [  12,   14,   41,    9, 5182,   12,   34,   27,  347,  164],
       [  27,   15,   30,  168,   53, 4444,   75,   14,  535,   60],
       [  30,   15,   42,    3,   44,   97, 5552,    3,  131,    1],
       [  21,   10,   51,   30,   49,   12,    3, 5684,  195,  210],
       [  17,   63,   48,   86,    3,  126,   25,   10, 5429,   44],
       [  25,   18,   30,   64,  118,   36,    1,  179,  371, 5107]],
      dtype=int64)

可以通过灰度图绘制出来：

plt.matshow(conf_mx,cmap=plt.cm.gray)
save_fig('confusion_matrix_plot', tight_layout=False)
plt.show()

image-20221101221248997

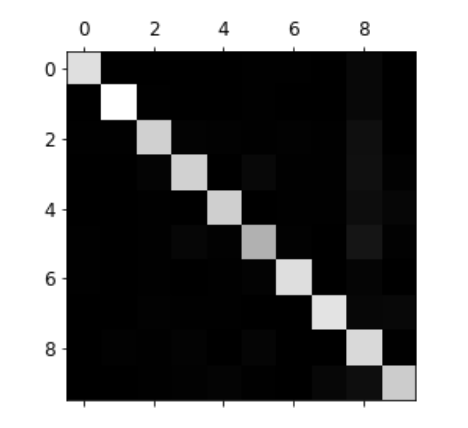
将矩阵每个数字除以每行总数（即实际上该行所指示类别的所包含的总和），并将对角线（正确分类的）设置为0，可以查看哪些类错误出现得最多（偏亮的）

image-20221101221643918

图中表现出5被错误分成8的次数很多

多标签分类与多输出分类

使用一些分类器可以实现标签的多个输出,比如KNeighbors方法

from sklearn.neighbors import KNeighborsClassifier
y_train = y_train.astype(np.uint8)
y_train_large =(y_train >=7)
y_train_odd = (y_train %2 ==1)
y_multilabel =np.c_[y_train_large,y_train_odd]

knn_clf =KNeighborsClassifier()
knn_clf.fit(X_train,y_multilabel)

而分类问题有时也可看做回归问题，我们将带有噪声的图片放入分类器中训练，对于同样带有噪音的测试集进行预测，这个过程是一种多输出分类，也像是回归的过程：

#构建噪音训练/测试集
noise = np.random.randint(0,100,(len(X_train),784))
X_train_mod =X_train+noise
noise=  np.random.randint(0,100,(len(X_test),784))
X_test_mod =X_test+noise
y_train_mod = X_train
y_test_mod = X_test

def plot_digit(data):
    image = data.reshape(28, 28)
    plt.imshow(image, cmap = mpl.cm.binary,
               interpolation="nearest")
    plt.axis("off")
some_index =0
plt.subplot(121); plot_digit(X_test_mod[some_index])
plt.subplot(122); plot_digit(y_test_mod[some_index])
save_fig('noisy_digit_example_plot')
plt.show()

构建的测试集：

image-20221101222259805

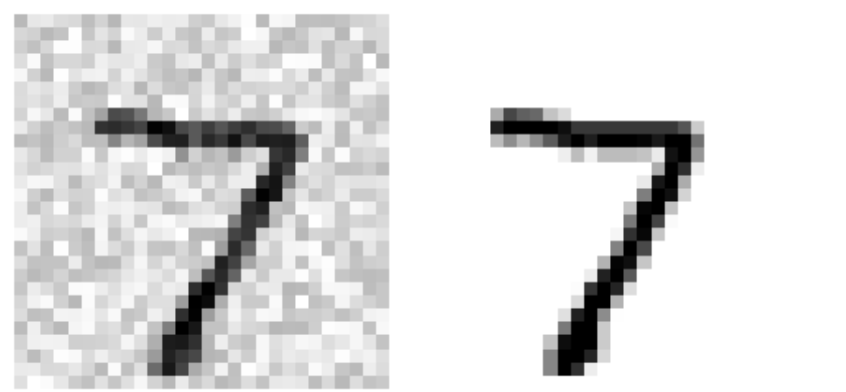
分类器进行的预测：

knn_clf.fit(X_train_mod, y_train_mod)
clean_digit = knn_clf.predict([X_test_mod[some_index]])
plot_digit(clean_digit)
save_fig("cleaned_digit_example_plot")

image-20221101222354260

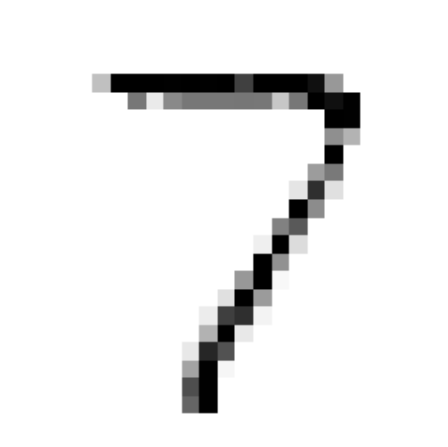
讨论

交叉验证过程中cross_val_score与cross_val_predict的使用

：得到K折验证中每一折的得分，K个得分取平均值就是模型的平均性能

cross_val_predict：得到经过K折交叉验证计算得到的每个训练验证的输出预测

参考

---

1. 1.机器学习笔记： 混淆矩阵 ↩︎
2. 2.多分类学习（OvO、OVR、MVM 原理区别） ↩︎