重新记一次机器学习训练过程

前言

最近重新捡起《机器学习实战：基于Scikit-Learn、Keras和TensorFlow》这本书，同时在整理西瓜书，以及白板推导的相关笔记，准备好好学习本科期间最想学习的机器学习，这篇文章按照原书的代码进行，一步步介绍机器学习的一般步骤。

本文，你即将掌握的知识：

  1. 机器学习处理实际数据将会采用的方法
  2. 数据处理过程中使用的重要函数的使用方法
  3. 评价模型性能的过程

处理过程

流程的数理

前面我提到了什么是机器学习，简述了机器学习的基本概念，这次我们将进行的是对实际数据进行处理，将数据进行合理的处理之后，定性了解数据包含的特性，随后选择合理的模型进行训练。

数据的获取

数据来自https://raw.githubusercontent.com/ageron/handson-ml2/master/datasets/housing/housing.tgz

解压后数据是housing.csv

数据探索

首先读取一下数据,写一个数据读取函数

1
2
3
4
5
import pandas as pd
def load_data(data_path):
    csv_path = os.path.join(data_path,"housing.csv")
    return pd.read_csv(csv_path)
load_data(data_path)

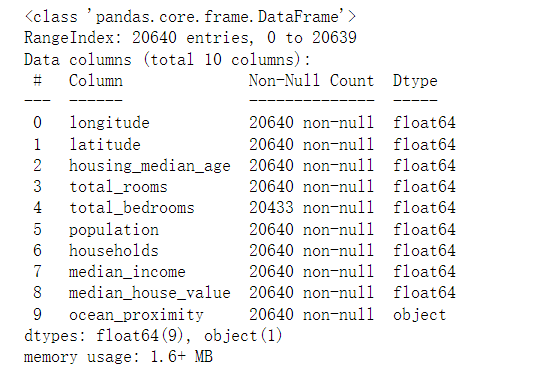
数据的基本信息：

info()：类型、数量

describe()：平均值、总和、标准差、最大最小、分段

value_counts()：每一类数据数目（定量角度）

hist()：直方图，定性

这里可以看到total_bedrooms存在缺失值，ocean_proximity不是数据类型

housing['ocean_proximity'].value_counts() 查看数据类型数目

ocean_proximity有5种类型

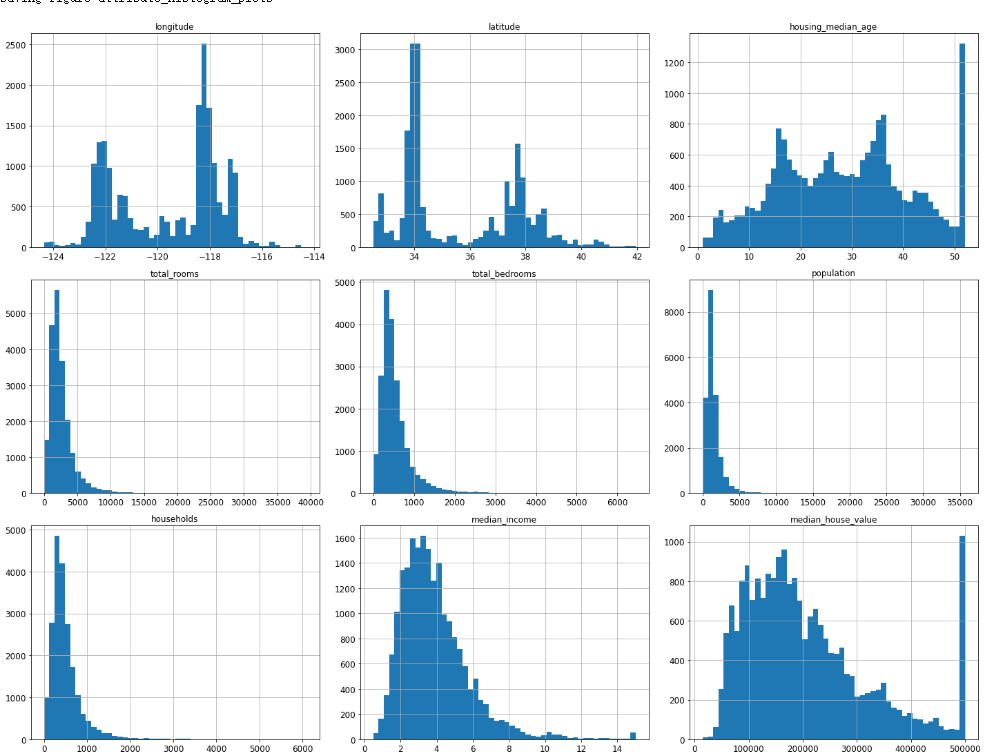
绘制直方图，数据探索的时候，可以直接对主要的数据进行直方图的绘制

1
2
3
housing.hist(bins=50,figsize=(20,15))
save_fig('attribute_histogram_plots')
plt.show()

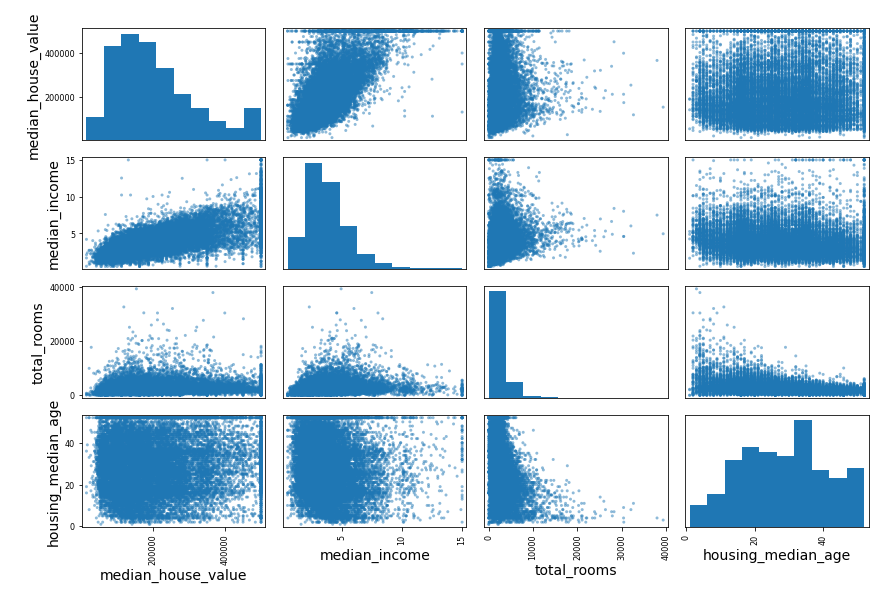
还可以看看数据的相关性：

1
2
3
4
5
6
from pandas.plotting import scatter_matrix

attributes =['median_house_value','median_income','total_rooms',
            'housing_median_age']
scatter_matrix(housing[attributes],figsize=(12,8))
save_fig("scatter_matrix_plot")

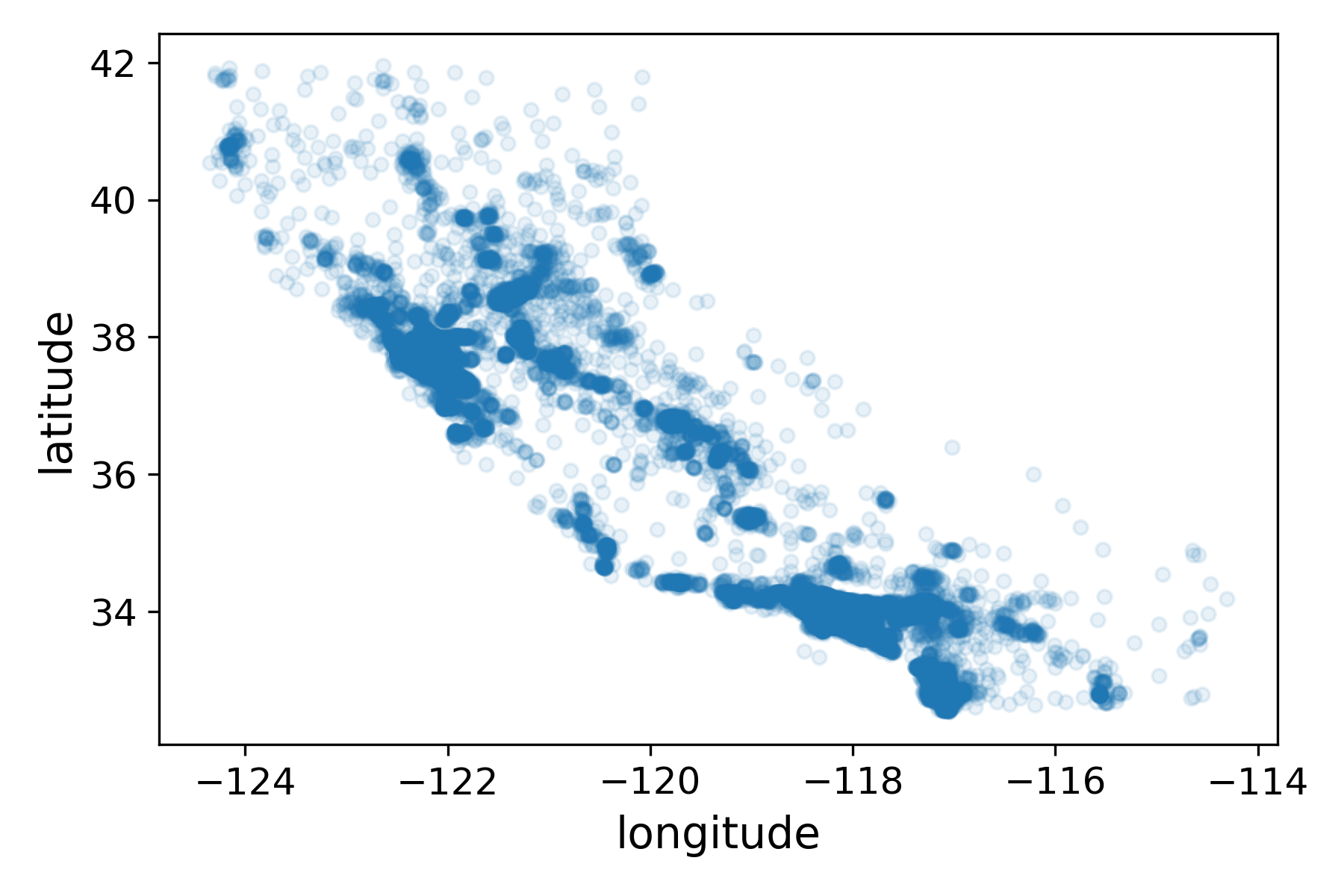
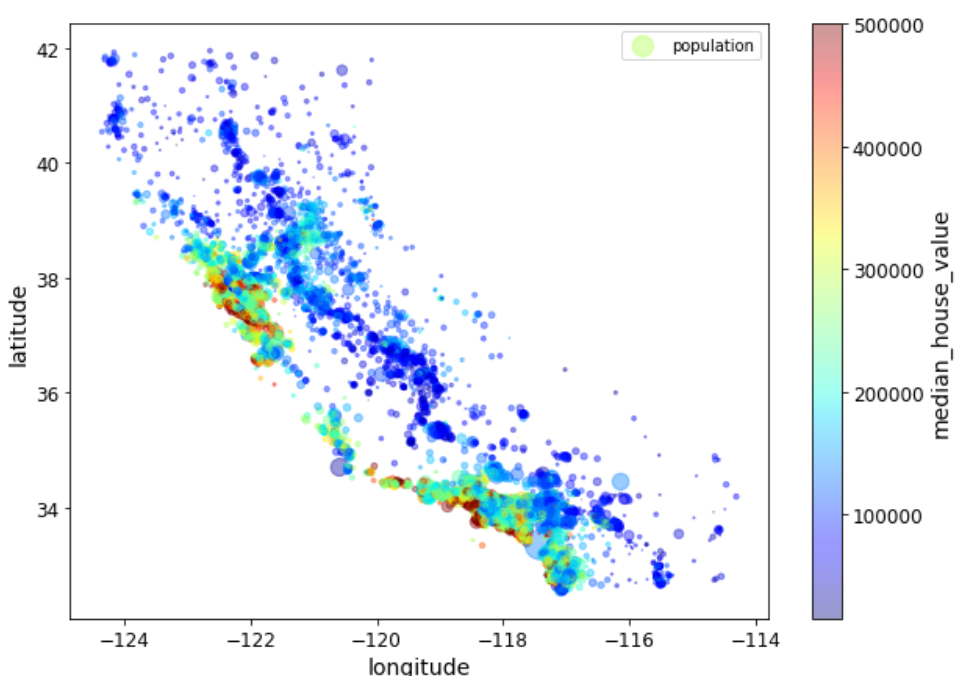
由于数据集中包含了地理信息，所以我们还可以查看数据中的地理信息：

1
2
housing.plot(kind="scatter",x="longitude",y="latitude", alpha=0.1)
save_fig("bad_visualization_plot")

1
2
3
housing.plot(kind="scatter",x="longitude",y="latitude",alpha=0.4,
            s=housing['population']/100,label="population",
             figsize=(10,7),c='median_house_value',cmap=plt.get_cmap("jet"),colorbar=True,sharex=False)

数据清洗

处理缺失值

这里采用的是中位数填补的方法：

1
2
3
4
housing = strat_train_set.drop("median_house_value",axis=1)
housing_labels = strat_train_set['median_house_value'].copy()
median = housing['total_bedrooms'].median()
housing['total_bedrooms'].fillna(median,inplace=True)

也可以用SimpleImputer()函数，SimpleImputer()的用法和很多sklearn模型一样，都有fit和transform的过程

1
2
3
4
from sklearn.impute import SimpleImputer
imputer =SimpleImputer(strategy="median")
imputer.fit(housing_num)
X =imputer.transform(housing_num)# 转换后的数据

独热编码

对于大部分机器学习模型的训练，都不能处理分类型的数据，所以对于上文提到的ocean_proximity，需要做一下转换：

1
2
3
4
housing_cat = housing[["ocean_proximity"]]
from sklearn.preprocessing import OneHotEncoder
cat_encoder = OneHotEncoder()
housing_cat_1hot = cat_encoder.fit_transform(housing_cat)

划分数据

一般数据并不是我们所想的那么均衡，可能依据合理指标进行分层划分比较合适。这里安装收入中位数为指标，划分不同人群。

1
2
3
housing["income_cat"]=pd.cut(housing["median_income"],
                            bins=[0.,1.5,3.0,4.5,6.,np.inf],
                            labels=[1,2,3,4,5])
1
2
3
4
5
6
from sklearn.model_selection import StratifiedShuffleSplit

split =StratifiedShuffleSplit(n_splits=1,test_size=0.2,random_state=42)
for train_index,test_index in split.split(housing,housing['income_cat']):
    strat_train_set = housing.loc[train_index]
    strat_test_set  = housing.loc[test_index]

我们可以看到分层抽样的效果

1
strat_test_set['income_cat'].value_counts()/len(strat_test_set)

模型训练

对模型进行训练，我们可以计算其RMSE、MSE或者使用交叉验证来对模型进行评估,这里展示的是每个模型10折交叉验证后的评分，分数越低越好

线性回归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score

def display_scores(scores):#这里定义一个展示评估模型性能的函数
    print("Scores:" ,scores)
    print("Mean:",scores.mean())
    print("Standard deviation:",scores.std())
display_scores(tree_rmse_scores)

lin_reg = LinearRegression()
lin_reg.fit(housing_prepared, housing_labels)
lin_scores =cross_val_score(lin_reg, housing_prepared, housing_labels, scoring="neg_mean_squared_error",cv=10)
lin_rmse_scores=np.sqrt(-lin_scores)
display_scores(lin_rmse_scores)
1
2
3
4
5
Scores: [66877.52325028 66608.120256   70575.91118868 74179.94799352
 67683.32205678 71103.16843468 64782.65896552 67711.29940352
 71080.40484136 67687.6384546 ]
Mean: 68828.99948449331
Standard deviation: 2662.761570610342

决策树

1
2
3
4
5
6
7
8
from sklearn.tree import DecisionTreeRegressor
from sklearn.model_selection import cross_val_score

tree_reg = DecisionTreeRegressor()
tree_reg.fit(housing_prepared,housing_labels)
scores =  cross_val_score(tree_reg, housing_prepared, housing_labels, scoring="neg_mean_squared_error",cv=10)
tree_rmse_scores = np.sqrt(-scores)
display_scores(tree_rmse_scores)
1
2
3
4
5
Scores: [69595.77288562 65892.49840035 68904.08708221 68631.79627553
 71158.28958246 75759.34692938 71756.17740938 69757.92410769
 77555.84660582 70320.51898092]
Mean: 70933.22582593601
Standard deviation: 3259.5535441625275

随机森林

1
2
3
4
5
6
7
8
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import cross_val_score
forest_reg =RandomForestRegressor()
forest_reg.fit(housing_prepared,housing_labels)
housing_predictions = forest_reg.predict(housing_prepared)
forest_scores = cross_val_score(forest_reg,housing_prepared,housing_labels,scoring="neg_mean_squared_error",cv=10)
forest_rmse_scores = np.sqrt(-forest_scores)
display_scores(forest_rmse_scores)
1
2
3
4
5
6
Scores: [49756.8518613  47523.28917137 49592.54848874 52307.84156741
 49780.9586572  53512.58220897 49036.6329955  48293.65141653
 52721.7847535  50370.22281034]
Mean: 50289.63639308592
Standard deviation: 1860.5796438282039

网格搜索

对于许多机器学习模型都会有很多参数可供调整和选择，但是并不是我最初设定或者默认的参数是最适合数据训练的，所以可以采取网格搜索或者随机搜索的方式进行训练。

网格搜索：

1
2
3
4
5
6
7
8
9
10
11
12
from sklearn.model_selection import GridSearchCV

param_grid=[
    {"n_estimators":[3 ,10, 30],'max_features': [2, 4, 6, 8]},
    {"bootstrap": [False],'n_estimators':[3,10],'max_features':[2, 3, 4]},
]
forest_reg = RandomForestRegressor(random_state=42)

grid_search = GridSearchCV(forest_reg,param_grid,cv=5,
                          scoring="neg_mean_squared_error",
                          return_train_score=True)
grid_search.fit(housing_prepared, housing_labels)

最佳参数组合：

1
grid_search.best_params_

最佳模型：

1
grid_search.best_estimator_

展示所有结果：

1
2
3
cvres = grid_search.cv_results_
for mean_score, params in zip(cvres["mean_test_score"],cvres["params"]):
    print(np.sqrt(-mean_score),params)

随机搜索：

1
2
3
4
5
6
7
8
9
10
11
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import randint

param_distribs = {
    'n_estimators': randint(low=1,high=200),
    "max_features": randint(low=1,high=8),
}
forest_reg = RandomForestRegressor(random_state=42)
rnd_search = RandomizedSearchCV(forest_reg,param_distributions=param_distribs,
                               n_iter=10,cv=5,scoring="neg_mean_squared_error",random_state=42)
rnd_search.fit(housing_prepared, housing_labels)

讨论

关于对分类型变量的处理

独热编码

对于存在N种类别的分类型数据，使用N位状态寄存器来对N个类型进行编码，每个状态都有它独立的寄存器位，并且在任意时候，其中只有一位有效。即，只有一位是1，其余都是零值。独热编码 是利用0和1表示一些参数，使用N位状态寄存器来对N个状态进行编码。

例如：

特征：["A"，"B"，"C"]（N=3，三维数据）： A => 100 B => 010 C => 001

优点

为什么要这么处理？因为在机器学习的很多算法中，都不能直接处理这种分类型数据，而算法对于特征之间距离的计算或相似度的计算存在一定的要求，而相似度的计算基于欧式空间进行，对变量进行独热编码处理，可以将原来不能处理的分类型数据扩展到欧式空间进行计算

缺点

但是问题在于假如分类型的变量变得非常多时，会使得独热编码生成的变量变得非常多

与哑变量处理的关系

哑变量处理与独热编码的原理差不多，区别在于[1]：

哑变量处理：具有k-1个二进制状态，基准类别将被忽略,若基准类别选择不合理，仍存在共线性，因此建议众数的类别为基准类别。

独热编码：具有k个特征二进制特征

用法辨析

对于定类变量 对数值大小较敏感的模型，如LR SVM a 哑变量的截距是基准类别的值，哑变量的回归系数表示的是某类别和基准类别之间的平均差异； b 若线性模型有截距项，用哑变量，因为多余的自由度可以被统摄到截距项intercept里去； c 若线性模型有截距项，且使用正则化，用独热编码，因为正则化会约束系数，使各变量地位相等，从而处理多余特征； d 无截距项，使用独热编码 e 树模型不建议使用二进制类型的编码，因为会加深树的深度，或者减小节点分裂增益

对于定序变量 既分类又排序，自定义的数字顺序可以不破坏原有逻辑，并与这个逻辑相对应。对数值大小不敏感的模型（如树模型）不建议使用one-hotencoding

选择建议：最好是选择正则化 + one-hot编码；哑变量编码也可以使用，不过最好选择前者。对于树模型，不推荐使用定类编码，因为样本切分不均衡时，增益效果甚微(如较小的那个拆分样本集，它占总样本的比例太小。无论增益多大，乘以该比例之后几乎可以忽略)；

参考

#机器学习
重新记一次机器学习训练过程
http://example.com/2022/10/22/2022-10-22-重新记一次机器学习训练过程/
作者
Brianyjh
发布于
2022年10月22日
许可协议